
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1557. Квадратура круга
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
— Извини, Теодор, но это ты очень странно рассуждаешь. Бессмыслица —– искать решение, если оно и так есть. Речь идёт о том, как поступать с задачей, которая решения не имеет. Это глубоко принципиальный вопрос, который, как я вижу, тебе, прикладнику, к сожалению, не доступен. Аркадий и Борис Стругацкие, «Понедельник начинается в субботу» Квадратура круга —– задача, заключающаяся в нахождении построения с помощью циркуля и линейки квадрата, равновеликого данному кругу (то есть имеющего ту же площадь, что и круг). Наряду с трисекцией угла и удвоением куба, эта задача является одной из самых известных неразрешимых задач на построение с помощью циркуля и линейки. Однако, задача о квадратуре круга становится разрешимой, если расширить средства построения, а также если искать не точное, а приближённое решение. В этой задаче требуется по кругу, заданному координатами центра и радиусом, построить квадрат, площадь которого отличается от площади этого круга не более чем на 10-6. В качестве средства предлагается использовать компьютер и один из доступных языков программирования. Напомним, что площадь квадрата со стороной a равна a2, а площадь круга радиуса r равна π·r2, где π≈3.1415926535897932384626433832795... — это половина длины окружности единичного радиуса. Входные данные В единственной строке входного файла заданы через пробел три целых числа x, y и r (|x|,|y|≤100, 1≤r≤100) — координаты центра круга и его радиус. Выходные данные Выведите в выходной файл четыре строки. Каждая строка должна содержать два числа через пробел — координаты одной из вершин квадрата. Найденный квадрат должен иметь стороны, параллельные осям координат, и площадь, равную площади данного круга, а его центр должен совпадать с центром круга. В первой строке выведите координаты левой нижней вершины квадрата, во второй — левой верхней, в третьей — правой верхней и в четвёртой — правой нижней вершины. Выводите вещественные числа как можно более точно! Допускается экспоненциальная форма вывода. При проверке ответов все проверки на равенство — сравнение координат точек и площадей квадратов — производятся с точностью до Пример Входные данные 2 3 5 Выходные данные -2.431134627264 -1.431134627264
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Задачи с соревнований и сборов / | Сборы в Перми 2009 / | 06.07.09 Большой контест / |
| 1556. E - Солдаты-самоубийцы | 1557. | 1558. G - Расписание | 1559. H - Изгрызенные книги |
| время генерации 0.093 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |
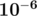 .
.