АВТ ВоГУ - Задача 1860. Змейка

Дана квадратная таблица A размера N × N, заполненная числами от 1 до N² в виде 'змейки', как показано на рисунке: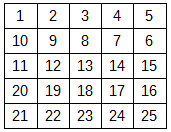

$\text{[math]}$

Требуется найти элемент на пересечении I-й строки и J-го столбца (нумерация строк и столбцов идёт с единицы). Например, для N = 5, I = 2, J = 4 получается A[2][4] = 7.

При использовании условного оператора эта задача решается очень просто. Попробуйте обойтись без него. Ваша задача — придумать формулу, выдающую верный ответ для любых N, I и J.

Выходные данные

Решением данной задачи должен быть текстовый файл (с расширением .txt), содержащий одну строку с формулой.

В формуле разрешено использовать только следующие элементы:

переменные N, I и J
целые числа в диапазоне от -1000 до 1000
круглые скобки
знаки операций +, -, *, /, %, где '+' означает сложение, '-' – вычитание, '*' – умножение, '/' – деление нацело (например, 5/3 = 1), '%' – остаток от деления (например, 5%3 = 2). Примечание: приоритет операций умножения, деления нацело и взятия остатка выше, чем у операций сложения и вычитания.

Длина формулы не должна превышать 255 символов. В процессе вычисления никакие промежуточные результаты не должны оказываться по модулю больше, чем 10⁹.

Пример решения:

((I + 1) / N + (I * J))%2 - 1

Примечание: данное решение неправильно

При отправке решения этой задачи на проверку в поле выбора языка следует выбирать 'Текст'.

Система оценки

Правильность вашей формулы будет проверяться подстановкой в неё десяти различных наборов значений N, I, J из диапазона от 1 ≤ I, J ≤ N ≤ 100. Каждый правильный ответ оценивается в 10 баллов.

Дистанционный практикум по программированию

1860. Змейка