В квадрат 3х3 в произвольном
порядке записали цифры от 1 до 9. Назовем квадрат магическим, если сумма любых его
строк и столбцов, а также диагоналей, одинакова (для нашего случая квадрата 3х3
эта сумма равна 15).
Разрешим производить циклический
сдвиг на одну клетку любой строки (влево или вправо) или любого столбца
квадрата (вверх или вниз). Обозначим эти операции следующим образом:
§
Dx – сдвиг вниз столбца x;
§
Ux – сдвиг вверх столбца x;
§
Lx – сдвиг влево строки x;
§
Rx – сдвиг вправо строки x.
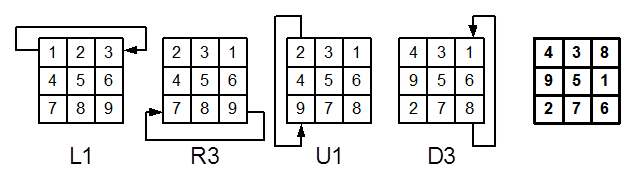
На рисунке ниже показан пример четырех
таких преобразований.
Напишите программу, которая
найдет минимальное количество сдвигов, необходимое для преобразования исходного
квадрата в магический.
Ограничения
Утверждается, что с помощью
операций циклического сдвига исходный квадрат всегда можно превратить в
магический.
Входные данные
Входной файл состоит из трех
строк, каждая из которых содержит по три числа, разделенных пробелами –
элементы квадрата.
Выходные данные
Первая строка выходного файла
должна содержать целое число n – количество
сдвиговых операций, необходимых для превращения исходного квадрата в магический.
Далее должны следовать n строк, каждая из
которых содержит код операции сдвига.
Номера строк и столбцов
записываются за символами «D», «U»,
«L» и «R» без пробела, и могут
принимать значения от 1 до 3. Строки квадрата нумеруются сверху вниз, столбцы –
слева направо.
Пример
|
Input
|
Output
|
|
1 2 3
4 5 6
7 8 9
|
4
L1
R3
U1
D3
|

