Let us consider
an example of long multiplication of four-digit decimal numbers (see a figure
below).
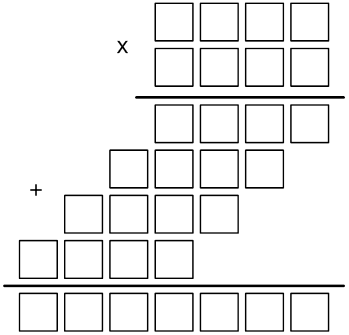
Each cell in the
figure corresponds to a certain decimal digit. It is unknown what digit goes to
each cell; however the total number of occurrences for each digit is given.
Write a program
that, given the number of
occurrences of each digit, will fill the cells in the
example, thus producing a correct long multiplication
whenever possible.
Example. Suppose we have 26 occurrences of digit
1, two 2’s and 3’s, and a single 4. In this case the cells may be filled in the
following manner:
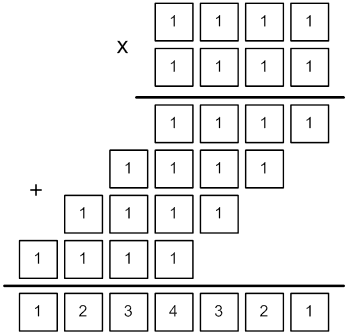
Input
The first line of
the input file contains ten space-delimited integers – the number of
occurrences of each decimal digit. The first integer (n0) is the number of 0’s, the second one (n1) is the number of 1’s, etc.
Limitations
0 <= ni <= 31, i=0..9;
 .
.
Output
The output file
should contain two lines with an integer number in each, describing the first
and the second multiplier, respectively. Leading zeros can be omitted.
If no solution
exists then both lines must contain “–1”
(without quotation marks).
Example
Input
|
Output
|
|
20 10 1
0 0 0 0 0 0 0
|
11
11
|
Input
|
Output
|
|
0 26 2 2 1 0 0 0 0
0
|
1111
1111
|
Input
|
Output
|
|
0 26 2 2 0 0 0 0 0
0
|
-1
-1
|


