Schoolboy Vasya enjoys challenging geometrical
problems. While reading an advanced-level math book he came across the
following problem.
Located along the horizontal axis of the
Cartesian plane, are k isosceles triangles. Bases of the
triangles lie on the X-axis, and the remaining vertexes are in the first
quadrant. The sides of adjoining triangles intersect (the right side of
triangle i intersects the left side of triangle i+1).
The left side of the first triangle intersects the Y-axis, and the right side
of the last triangle intersects the line x = n. So,
segments of triangle sides form a zigzag connecting the Y-axis on the left and
the line x = n on the right.
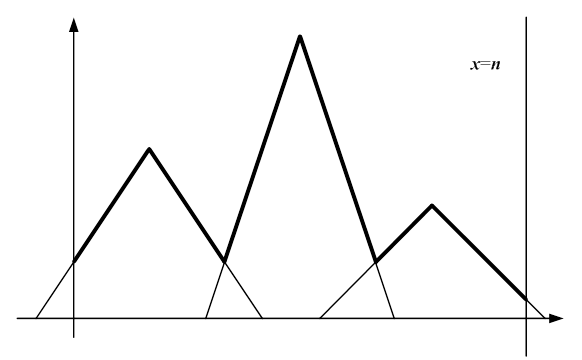
Let us define peaks as zigzag vertices
formed by upper triangle corners, and pits as remaining zigzag vertices,
formed by intersections. It is known that the coordinates of all zigzag
vertices—peaks and pits—are nonnegative integers.
A question arises—how many different zigzag
lines exist for given peak (not pit) coordinates? Help Vasya by writing program
that will answer this question.
Limitations
1 <= n <= 3 000; 2 <= k <= 500;
1 <= xi <= 3 000; 1 <= yi <= 1 000; xi
+ 1< xi+1, i = 1…k.
Input
The first line contains two space-delimited integers, n (the X-coordinate of the line (x
= n), and k
(the number of triangles). The following k lines carry
space-delimited pairs <xi, yi>, the coordinates
of peaks, one pair per
line.
Output
The output file should contain a single integer k, the number
of different zigzag lines modulo 230.
Example
Input
|
Output
|
|
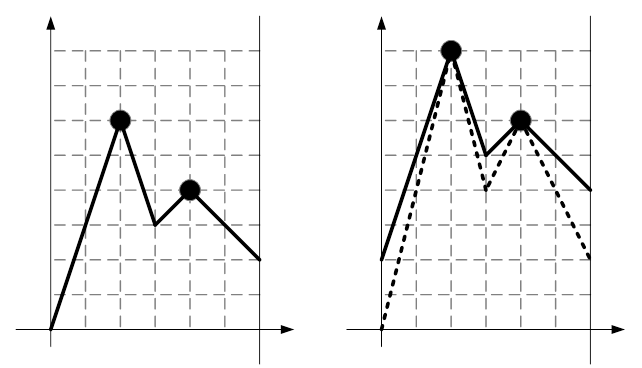
6 2
2 6
4 4
|
1
|
Input
|
Output
|
|
6 2
2 8
4 6
|
2
|
All Rybinsk-2012 problems (in PDF)


