
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1864. Мобильная связь
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
Через отдалённую местность проходит автомобильная трасса. На карте трасса выглядит как прямая линия, совпадающая с осью OX. В некоторых точках этой трассы установлено N станций сотовой связи. Каждая станция имеет одинаковый радиус действия, равный R. В окрестностях трассы находятся M деревень. Размеры всех деревень столь малы, что их можно считать точками. Будем говорить, что деревня входит в зону действия станции, если расстояние от этой деревни до станции не превышает R. Определите для каждой станции, сколько деревень входят в её зону действия. Входные данные В первой строке входных данных записаны три натуральных числа N, M и R — число станций, число деревень и радиус действия станций. В следующих N строках записано по одному целому числу в порядке возрастания — x-координаты станций (все их y-координаты равны нулю). В следующих M строках записано по два целых числа — координаты x и y каждой деревни. Никакие две деревни не находятся в одной точки. Все координаты не превосходят по модулю 109. Выходные данные Выведите N целых чисел, каждое в отдельной строке — количество деревень в зоне действия первой, второй и так далее станций. Система оценки Подзадача 1 (40 баллов): 1 ≤ N, M ≤ 1000, 1 ≤ R ≤ 109 Подзадача 2 (30 баллов): 1 ≤ N, M ≤ 105, 1 ≤ R ≤ 500 Подзадача 3 (30 баллов): 1 ≤ N, M ≤ 105, 1 ≤ R ≤ 109 Пример Входные данные 2 3 3 Выходные данные 2 Примечание Ниже приведена иллюстрация к примеру из условия. 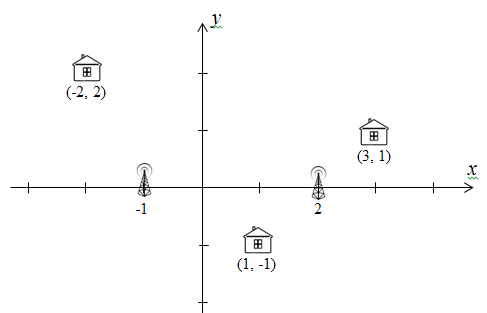 Здесь одна из деревень попадает в зону действия обеих станций, поэтому при подсчёте она учитывается для каждой станции.
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| 1863. 4 - Бери больше | 1864. |
| время генерации 0.109 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |