
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1727. Пирамиды
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
Будем говорить, что последовательность чисел a1, a2, ..., an является пирамидальной, если ai ≤ a⌊i / 2⌋ для всех i > 1 (где запись ⌊⌋ означает округление вниз). Например, последовательность Определите, сколько существует перестановок натуральных чисел от 1 до N, образующих пирамидальную последовательность. Поскольку ответ может быть достаточно большим, выведите его по модулю 2 × 109 + 17. Входные данные Натуральное число N (1 ≤ N ≤ 1000). Выходные данные Количество пирамидальных последовательностей, взятое по модулю 2 × 109 + 17 Пример Входные данные 4 Выходные данные 3
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Задачи с соревнований и сборов / | Межвузовские олимпиады / | XX межвузовская олимпиада - 2017 / |
| 1726. G - Ботанический сад | 1727. | 1728. I - Цепные дроби | 1729. J - Склад |
| время генерации 0.11 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |
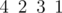 — пирамидальная, поскольку
— пирамидальная, поскольку