
|
Remote Training on Programming
|
||||||||||
|
|
|||||||||||
| Hello, Guest! Please login or register. |
1552. A+B
|
| View Problem Statistics | Submit | Problem added debug |
|
— Не комплексуй! из письма Пи к i Когда один известный алгебраист (далее — О. И. А.) с мат-меха был маленьким, ему в школе строго-настрого запретили брать квадратные корни из отрицательных чисел. Конечно же, О. И. А. на запрет наплевал и даже (о, ужас!) стал использовать то, что получается после взятия такого корня, в качестве основания системы счисления. Недавно О. И. А. нашёл свои старые записи, а в них какое-то подозрительное тождество. Чтобы проверить его справедливость, О. И. А. достаточно сложить два числа и посмотреть на результат. Но, к сожалению, эти два числа записаны как раз в системе счисления с основанием, равным корню из отрицательного числа (а конкретно, Как известно, мнимые числа — это как раз те числа, которые получаются в результате взятия квадратного корня из отрицательного числа. В системе с мнимым основанием Несмотря на то, что операция взятия корня из отрицательного числа неоднозначна (как Входные данные В первой строке входного файла задано число A, во второй — число B. Их длины не превосходят 1000000. Числа даны в системе счисления с основанием Выходные данные В единственной строке выходного файла должно быть выведено число A+B, записанное в системе счисления с основанием Примеры Входные данные 2 Выходные данные 10301 Входные данные 210 Выходные данные 1030023
|
| View Problem Statistics | Submit | Problem discussion | Author/source: |
| Problems from Contests and Camps / | Trainings in Perm 2009 / | 06.07.09 Big Contest / |
| 1552. | 1553. B - Circuit | 1554. C - Jack Joker | 1555. D - Lecture |
| time generating 0.094 sec. |
| © Copyright VSU, AVT, Nosov D.A., Andrianov I.A. |
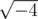 ), и ответ тоже должен быть представлен в системе счисления с основанием
), и ответ тоже должен быть представлен в системе счисления с основанием 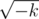 в числах используются цифры от
в числах используются цифры от 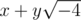 , где
, где 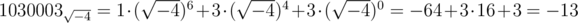 .
.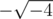 дают в квадрате
дают в квадрате