A very simple
technique is often used to pack complete binary trees. Consider 2n–1
nodes of a complete binary tree. We will put them into an array
T[1..2n–1] according to the following rules:
1.
the root is located in the first element.
2.
if a node is located in element i
then its descendants will be located in elements 2i and 2i+1
(left and right descendant, respectively).
Such packing is
similar to level packing: the first level (root) is written first followed by
the nodes of the second level (left-to-right), the nodes of the third level and
so on. A binary search tree and its array packing is shown in the figure.
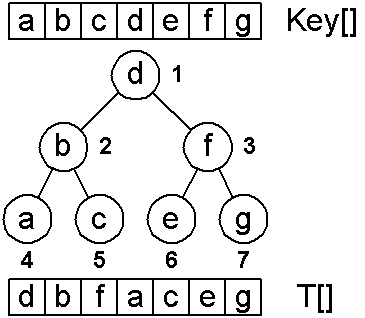
Let us remind
that a search tree is a tree such that for any node Node(i) with
key Key(i) the following property stands true: the keys of all
nodes from the left subtree are lexicographically less than Key(i),
while the keys of nodes from the right subtree are lexicographically greater
than Key(i). The case of equal keys is not considered.
Let us have an
array of 2n–1 keys Key[1..2n–1] in the
ascending order. For example, the keys shown in the figure will form an array
Key[1..7] in the following order: "a", "b", "c",
"d", "e", "f", "g". By matching arrays
Key[1..2n–1] and T[1..2n–1] we can say that
the elements "a", "b", "c" having numbers
(indices) 1, 2 and 3 take positions 4, 2, 5 in array T, respectively.
Write a program
that will determine the positions in array T[1..2n–1] for selected
elements from array Key[1..2n–1]
Limitations
1 <= n <= 1024; 1 <= m <= 104.
1 <= ki, zi
<= 2n–1,
i = 1, 2, … m.
Input
The first line
of the input file contains two integers n and m
separated by spaces. Then m lines follow, each containing number ki
in hexadecimal format. Number ki is the
position of a key in array Key.
Output
The first line
of the output file contains number m. Then m lines
follow, each containing a hexadecimal number zi,
the position of the key Key[ki] in array T[1..2n–1].
Numbers zi must not contain leading zeroes.
Sample
|
Standard input
|
Standard output
|
|
3 3
1
2
3
|
3
4
2
5
|

