
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1946. Высота дерева
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
Одним из способов представления множества в памяти машины является двоичное (бинарное) дерево поиска. Каждый узел данного дерева может иметь не более двух детей (левого и правого сына). Для любого узла r выполняется следующее свойство: ключи во всех узлах левого поддерева r меньше, чем ключ в узле r, а ключи в узлах правого поддерева – больше, чем в r. Вставка нового элемента x в дерево начинается с корневого узла. Сравним x с ключом в корне. Если они равны, то делать ничего не надо – вставка закончена. Если x меньше ключа в корне, то идём в левое поддерево, если больше – в правое. Продолжаем делать так до тех пор, пока идти станет больше некуда – в этом случае создаём новый листовой узел. На рисунке показано дерево, полученное из пустого дерева после вставки элементов 8, 5, 7, 11, 9, 3, 6. 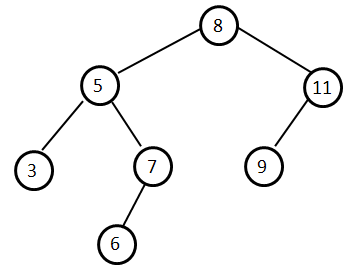 Высотой дерева называется длина максимального пути от корня до листа. Например, для дерева на рисунке высота равна 3, так как путь от от корня до листа с ключом 6 имеет длину 3. Вам дана последовательность элементов, которые поочерёдно вставлялись в изначально пустое дерево. Требуется найти его высоту. Входные данные В первой строке входных данных записано целое число N (1 ≤ N ≤ 1000) – количество элементов. В следующей строке через пробел записаны N целых чисел – вставляемые элементы (все элементы не превышают по модулю 109). Выходные данные Выведите одно целое число – высоту дерева. Примеры Входные данные 7 Выходные данные 3 Входные данные 3 Выходные данные 0 |
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Учебные курсы / | Алгоритмы и структуры данных / | Структуры данных / |
| 695. Близкие числа | 1946. | 245. Делители | 1947. Дерево по уровням | 243. Деревья |
| Учебные курсы / | Язык программирования C++ / | Структуры данных и использование указателей / |
| 1946. | 1947. 2 - Дерево по уровням | 253. 3 - Луч |
| время генерации 0.375 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |