
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1798. Пропавший путь
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
Вася – известный (в своей школе) разработчик компьютерных игр. В настоящее время он работает над программой, позволяющей создавать карты лабиринтов для очередной игры. Карта лабиринта представляет собой клетчатое поле размером N × M клеток. Вход в лабиринт находится в левой верхней клетке (с координатами 1, 1 ), выход – в правой нижней клетке (с координатами N, M ). Каждая клетка поля может быть или пустой, или закрашенной. Пустая клетка обозначает свободное место, закрашенная – непроходимую стену. Из одной пустой клетки можно перейти в другую, если они имеют общую сторону. За пределы лабиринта выходить нельзя. Программа Васи работает следующим образом. Вначале все клетки пусты. На каждом шаге он выбирает какую-то пустую клетку и щёлкает по ней мышкой, в результате клетка закрашивается. Через несколько таких шагов карта лабиринта готова. Теперь Вася хочет добавить в свою программу проверку, будет ли полученный лабиринт проходимым. Лабиринт является проходимым, если существует хотя бы один путь из левой верхней клетки в правую нижнюю. Если же пути не существует, то Вася хочет узнать номер первого шага, после которого это произошло. Помогите Васе решить данную задачу. Входные данные В первой строке входных данных записаны через пробел три числа N, M и K – размеры поля (число строк и столбцов) и количество закрашенных клеток. В следующих K строках записаны через пробел пары чисел Yi и Xi – координаты очередной закрашиваемой клетки (номер строки и номер столбца). Гарантируется, что Вася щёлкал только по пустым клеткам. Выходные данные Выведите одно число – номер первого шага, после которого лабиринт стал непроходимым. Если же лабиринт остался проходимым после всех закрашиваний, то выведите 0 (ноль). Система оценки Подзадачи: 1 ≤ N, M ≤ 20, 1 ≤ K ≤ N × M – 30 баллов, 20 < N, M ≤ 500, 1 ≤ K ≤ 100 – 30 баллов 20 < N, M ≤ 500, 100 < K ≤ N × M – 40 баллов Пример Входные данные 3 4 5 Выходные данные 4 Примечание Рисунок к примеру из условия (цифры показывают, в каком порядке закрашивались клетки): 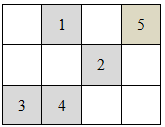
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Задачи с соревнований и сборов / | Школьные олимпиады и курсы Вологодской области / | ВсОШ, муниципальные этапы / | Муниципальный этап 2017-18 / | Классы 9-11 / |
| 1797. 3 - Сортировка | 1798. | 1799. 5 - Новогодний хоровод |
| время генерации 0.094 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |