Имеется телекоммуникационная сеть, состоящая из N
узлов. Некоторые пары узлов соединены каналами связи, для каждого канала
известна его пропускная способность в обоих направлениях. Требуется найти путь
для передачи трафика между двумя заданными узлами, имеющий максимальную
пропускную способность. Пропускная способность пути равняется минимальной
пропускной способности среди всех каналов (в соответствующем направлении),
через которые он проходит.
Формат входных и выходных данных
В первой строке входных
данных записаны через
пробел четыре целых числа — N, M, a
и b (2 ≤ N ≤ 1000, 0 ≤ M ≤ 10 000, 1 ≤ a, b ≤ N,
a ≠ b). Здесь N
— количество узлов, M — количество каналов связи, a и b —
номера начального и конечного узла.
В каждой из следующих M строк записано по 4
разделенных пробелами целых числа u, v,
c1, c2 (1 ≤ u < v ≤ N,
1 ≤ c1, c2 ≤ 1 000 000),
где узлы u и v —
концы очередного канала связи, c1 — пропускная способность в направлении от u
к v, c2 — пропускная способность в направлении от v
к u. Любые два узла соединены не более чем одним каналом.
В первой строке выходных
данных выведите одно целое
число — пропускную способность наилучшего пути. Если пути от a к b
не существует, выведите 0. Если же путь существует, выведите в следующей строке
через пробел номера узлов в порядке следования (первым узлом должен быть a,
последним — b). Если подходящих путей несколько, то выведите путь с
наименьшим количеством рёбер (каналов). Если таких путей также окажется больше
одного, то выведите любой.
Пример
|
Входные данные
|
Выходные данные
|
|
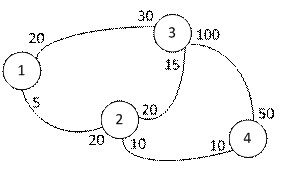
4 5 1 2
1 3 20 30
3 4 100 50
2 3 20 15
1 2 5 20
2 4 10 10
|
15
1 3 2
|
Примечание. На рисунке далее приведён граф сети для данного
примера (число на ребре рядом с каждой вершиной показывает пропускную
способность канала в направлении от неё).
Условия всех задач XVI межвузовской олимпиады в одном файле

