Let there be N
nondegenerate rectangles with sides parallel to coordinate axes. It is known
that the borders of these rectangles do not intersect and there are no identical
borders.
Let us say that
rectangle A is nested inside rectangle B if any point belonging to A
also belongs to B, and A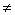 B.
B.
Let us say that
rectangle A is immediately nested inside rectangle B if A is nested
inside B and A is not nested inside any other rectangle that is nested inside
B.
Write a program
to analyse immediate nesting of rectangles.
Îãðàíè÷åíèÿ
1 <= N <= 100 000;
0 <= xij, yij
< 231 – coordinates of the opposite vertices of a rectangle.
Input
The first line
of the input file specifies an integer N. Then N
lines follow. Of these lines, line number i specifies 4 integers:
xi1, yi1,
xi2, yi2—the
coordinates of the opposite vertices of the i-th rectangle.
Output
Write N
lines to the output file. Line number i must contain the number
of a rectangle inside which rectangle number i is immediately
nested, or 0 if there is no such rectangle in the input set.
Sample
|
Standard input
|
Standard output
|
|
5
0 0 10
10
1 2 4 5
2 3 3 4
7 7 8 8
0 11 1
12
|
0
1
2
1
0
|
