
|
Remote Training on Programming
|
||||||||||
|
|
|||||||||||
| Hello, Guest! Please login or register. |
2167. Rook Route
|
| View Problem Statistics | Submit | Problem added debug |
|
На клетчатом поле размера $$$n \times n$$$ в клетке с координатами $$$x$$$, $$$y$$$ стоит ладья. За один ход ладья может переместиться на любое число клеток по горизонтали или вертикали. Требуется посетить все клетки на поле, сделав минимальное количество ходов. При выполнении хода посещёнными считаются не только начальная и конечная клетки, но также и промежуточные. Разрешается посещать клетки более одного раза. Входные данные Во входных данных записаны 3 числа — $$$n$$$, $$$x$$$ и $$$y$$$, каждое в отдельной строке ($$$x$$$ — горизонтальная координата ладьи, $$$y$$$ — вертикальная). Ограничения: $$$2 \le n \le 50$$$, $$$1 \le x, y \le n$$$. Выходные данные Выведите координаты ладьи $$$x_i$$$ и $$$y_i$$$ после каждого хода. Каждая пара координат выводится в отдельной строке, числа в парах разделяются пробелом. Если имеется несколько правильных ответов, выведите любой. Пример Входные данные 3 1 2 Выходные данные 3 2 3 1 1 1 1 3 3 3 Примечание Иллюстрация к примеру из условия: 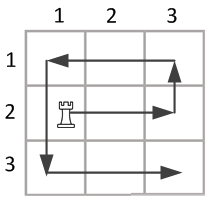 Система оценивания: Подзадача 1 (до 24 баллов): $$$x = y = 1$$$. Подзадача 2 (до 28 баллов): $$$x = 1$$$ или $$$y = 1$$$. Подзадача 3 (до 48 баллов): дополнительных ограничений нет. |
| View Problem Statistics | Submit | Problem discussion | Author/source: |
| Problems from Contests and Camps / | School olympiads and couses of Vologda region / | All-Russian school olympiad, municipal stage / | Municipal Stage 2022-23 / | Forms 9-11 / |
| 2166. 4 - Numbers with different digits | 2167. |
| time generating 0.125 sec. |
| © Copyright VSU, AVT, Nosov D.A., Andrianov I.A. |