|
В некотором городе есть метро, состоящее из N (1 <= N <= 1000) станций и M линий, соединяющих их. Каждая линия обеспечивает проезд между какими-то двумя станциями в обе стороны. Между любой парой станций проведено не более одной линии. Сеть метро построена таким образом, чтобы с каждой станции можно было проехать на каждую (возможно, через промежуточные станции). Назовем это свойство связностью метро.
В связи с изобретением принципиально нового вида транспорта метро стало убыточным, и его работу решили прекратить. На заседании мэрии города было постановлено закрывать каждый год по одной станции, но так, чтобы связность метро каждый раз сохранялась. При закрытии какой-либо станции, линии, ведущие из этой станции в другие, естественно, тоже перестают функционировать.
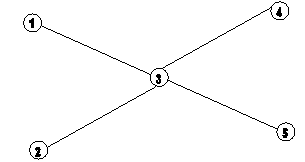
Задание. По введенной информации о сети метро разработать какой-либо порядок закрытия станций, при котором метро всегда будет оставаться связным. Например, пусть метро выглядит так, как показано на рисунке. Тогда станции можно закрывать, например, в порядке 1, 2, 4, 3, 5. А порядок 3, 1, 2, 4, 5 - не подходит, так как после закрытия 3-й станции метро распадется на четыре не связных между собой части.
Ввод. Первая строка входного файла будет содержать числа N и M. В следующих M строках находится информация о линиях. Каждая из этих строк содержит через пробел числа Ai и Bi (Ai Bi) - две станции, которые соединяет i-я линия.
Вывод. Выходной файл должен состоять из N строк. Каждая строка должна содержать одно число - номер станции. Вывести станции нужно в порядке их закрытия.
Пример
input
5 4
3 1
3 2
3 4
3 5
output
1
2
4
3
5
|

