
|
Remote Training on Programming
|
||||||||||
|
|
|||||||||||
| Hello, Guest! Please login or register. |
1852. Shortest path
|
| View Problem Statistics | Submit | Problem added debug |
|
Студент Василий живёт в городе, где улицы образуют правильную сетку кварталов: все кварталы являются квадратами с длиной стороны, равной 100 метрам. Дом Василия располагается в юго-западном углу – точке с координатами (0, 0). Университет располагается в северо-восточном углу – точке с координатами (N, M). 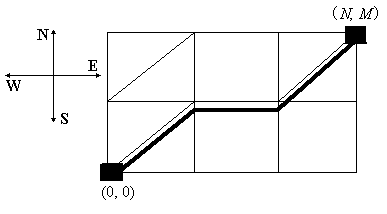 Выйдя утром из дома, Василий идёт в университет. Он движется по улицам, но при этом некоторые кварталы может пересечь также по диагонали, ведущей из юго-западного угла квартала в северо-восточный. Напишите программу, которая вычислит длину кратчайшего маршрута от дома до университета. Входные данные В первой строке находятся два целых числа N и M (0 < N, M ≤ 109) – размер сетки кварталов с запада на восток (по горизонтали) и с юга на север (по вертикали) соответственно. Во второй строке находится целое число K (0 ≤ K ≤ 105) – количество кварталов, через которые можно пройти наискосок. Далее следуют K строк с парами целых положительных чисел x и y, разделённых пробелами – координаты северо-восточных углов таких кварталов (1 ≤ x ≤ N, 1 ≤ y ≤ M). Выходные данные Требуется вывести длину кратчайшего пути от дома Василия до университета в метрах, округлённую до ближайшего целого. Пример Входные данные 3 2 Выходные данные 383 |
| View Problem Statistics | Submit | Problem discussion | Author/source: |
| Problems from Contests and Camps / | Vologda Students Contests / | XXI Interuni Olympiad - 2018 / |
| 1851. F - Pascal triangle | 1852. | 1853. H - Binary tree | 1854. I - Weights | 1855. J - Search Index |
| Problems from Contests and Camps / | School olympiads and couses of Vologda region / | Impulse - 2019 / | Segment Trees / |
| 1986. 09 - Tickets to Train | 1852. |
| time generating 0.313 sec. |
| © Copyright VSU, AVT, Nosov D.A., Andrianov I.A. |