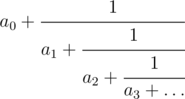|
Remote Training on Programming
|
||||||||||
|
|
|||||||||||
| Hello, Guest! Please login or register. |
1808. Quadratic Equation
|
| View Problem Statistics | Submit | Problem added debug |
|
Цепная дробь (или непрерывная дробь) – это математическое выражение вида
где a0 – целое число, все остальные элементы ai – положительные целые числа. Для удобства такую дробь можно записать следующим образом: [a0;a1, a2, a3, ...] Бесконечная цепная дробь, в которой определенная последовательность элементов, начиная с некоторого места, периодически повторяется, называется периодической. Если периодическое повторение начинается сразу с элемента a1 (то есть отсутствует предпериод), то такая дробь называется чисто периодической. Общеизвестно, что между периодическими цепными дробями и квадратичными иррациональностями существует взаимно однозначное соответствие. Вам предлагается по данной чисто периодической цепной дроби найти коэффициенты квадратного уравнения, корнем которого является квадратичная иррациональность, соответствующая данной периодической цепной дроби (гарантируется, что для приведённых входных данных все коэффициенты уравнения могут быть целыми). Входные данные В первой строке входных данных записано положительное целое число N. Далее идут N + 1 чисел (на первом месте целая часть цепной дроби, далее числа периода). Гарантируется, что все числа ввода натуральные и не превосходят 250. Выходные данные В ответе напечатайте 3 целых числа - коэффициенты квадратного уравнения, соответствующего данной цепной дроби (в порядке убывания показателей степеней), причём коэффициент старшего члена должен быть положительным, а сами коэффициенты взаимно простыми. Пример Входные данные 2 Выходные данные 1 0 -3
|
| View Problem Statistics | Submit | Problem discussion | Author/source: |
| Problems from Contests and Camps / | School olympiads and couses of Vologda region / | Different Contests / | VML Open Code Cup (November 2017) / |
| 1807. 3 - Rectangular parallelepipeds | 1808. | 1809. 5 - Sale of cucumbers |
| Problems from Contests and Camps / | School olympiads and couses of Vologda region / | Impulse - 2019 / | Number Theory / |
| 1866. 10 - Flowers | 1808. | 1744. 12 - Numbers with Small Prime divisors | 1749. 13 - Sum of Squares |
| Problems from Contests and Camps / | School olympiads and couses of Vologda region / | Impulse, september 2020 / | Impulse-2020, number theory / |
| 1739. 08 - Euler Function | 1808. | 1744. 10 - Numbers with Small Prime divisors | 1749. 11 - Sum of Squares |
| time generating 0.109 sec. |
| © Copyright VSU, AVT, Nosov D.A., Andrianov I.A. |