|
Remote Training on Programming
|
||||||||||
|
|
|||||||||||
| Hello, Guest! Please login or register. |
1230. Logic circuit
|
| View Problem Statistics | Submit | Problem added Игорь Андрианов |
|
Как известно, любую логическую функцию от N переменных можно реализовать цифровой электронной схемой, используя только логические элементы "И-НЕ". Примечание: логический элемент «И-НЕ» выполняет операцию «логическое И» над входными сигналами и инвертирует результат. На практике желательно учитывать, что реальные логические элементы обрабатывают смену входных сигналов с некоторой задержкой. Соответственно, при последовательном подключении элементов (т.е. выход первого на вход второго) эта задержка суммируется. Требуется написать программу, строящую схему для заданной логической функции f(x1, …, xN). Построенная схема должна обладать минимальной задержкой — то есть путь максимальной длины от одного из входов схемы к её выходу должен быть как можно короче. Схема должна представлять собой ациклический ориентированный граф с тремя типами вершин: 1. Вершины-элементы «И-НЕ». В каждую такую вершину должно входить ровно две дуги, а выходить может одна или более (тем самым обеспечивается возможность разветвления выходного сигнала). Данные вершины нумеруются последовательными целыми числами 1, 2, …, M (где M — общее количество элементов «И-НЕ»). 2. N вершин-входов. В данные вершины не должны входить дуги, а выходить из каждой может ноль и более дуг. Данные вершины нумеруются отрицательными целыми числами от –N до –1. Каждой входной переменной xi соответствует вершина с номером –i. 3. Одна вершина-выход. Из неё не должны выходить дуги, а входить в неё должна ровно одна дуга. Данная вершина имеет номер 0. Несложно заметить, что общее количество дуг в таком графе будет равняться 2 M + 1. Формат входных и выходных данных В первой строке входных данных записано целое число N — количество переменных (1 ≤ N ≤ 3). В следующей строке через пробел записаны 2N чисел 0 или 1 — значения функции f на каждом возможном наборе входных переменных x1, …, xN (наборы упорядочены лексикографически). В первой строке выходных данных выведите через пробел два целых числа M и Q, где M — количество использованных элементов «И-НЕ» (0 ≤ M ≤ 100), Q — количество элементов «И-НЕ» в максимальном пути в графе. В каждой из следующих 2M + 1 строк выведите через пробел два целых числа в диапазоне от –N до M — начало и конец очередной дуги. Если имеется несколько верных ответов, то выведите любой, дуги можно выводить в любом порядке. Примеры
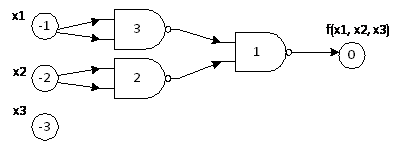
Пояснения к примерам В первом примере функция
Построенная для данной функции схема изображена на рисунке.
Во втором примере не используется ни одного элемента «И-НЕ» — входной сигнал x1 подключен сразу к выходу схемы.
|
| View Problem Statistics | Submit | Problem discussion | Author/source: |
| Problems from Contests and Camps / | Vologda Students Contests / | XVI InterUni Olympiad 2013 / |
| 1229. J - Synonyms | 1230. |
| time generating 0.125 sec. |
| © Copyright VSU, AVT, Nosov D.A., Andrianov I.A. |