Горнолыжная трасса представляет собой
последовательность чередующихся спусков и подъёмов. Для всех точек трассы, где
спуск меняется на подъём (или наоборот), известна высота над уровнем равнины.
Начальная и конечная точка трассы имеют высоту 0.
Руководство одной секретной организации решило
провести на этой трассе для своих секретных агентов тренировки по катанию на
горных лыжах. Однако, агенты в этой организации настолько секретные, что они
не должны даже встречаться друг с другом. Поэтому было принято решение выделить
каждому агенту свой участок трассы (участком назовём часть трассы между двумя
соседними отметками высот), причём так, чтобы на соседних участках слева и
справа от него агентов не было.
Требуется определить, для какого максимального числа
агентов одновременно можно провести тренировки.
Кроме того, найденное максимальное число агентов нужно
разместить на трассе так, чтобы сумма модулей перепадов высот на их участках
получилась максимально возможной.
В первой строке входных данных записано одно целое
нечётное число N – количество промежуточных точек трассы (начальная и конечная
точка всегда равны нулю и поэтому не вводятся, 1 ≤ N < 100).
В следующей строке через пробел записаны N целых чисел
hi – высоты точек при движении слева направо (0 ≤ hi
≤ 10000). Гарантируется, что никакие три последовательных значения высот
не возрастают и не убывают, горизонтальных участков на трассе нет.
Выведите два числа через пробел – максимально
возможное количество агентов и максимально возможную при этом сумму взятых по
модулю перепадов высот назначенных агентам участков.
|
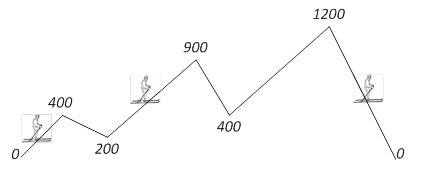
Пример ввода 1 (см. рисунок)
5
400 200 900 400
1200
Пример вывода 1
3
2300
|
Пример ввода 2
3
10000
0 10000
Пример вывода 2
2
20000
|

