|
English Russian |
Практикум по программированию |
| Вы не вошли в систему! Вход или регистрация. |
Последняя вершина
| Time limit: | 1 sec. |
| Memory limit: | 262144 KByte |
Как известно, для хранения дерева отрезков, построенного для входного массива размера N, достаточно создать массив размером не более 4·N. Заметим, что величина 4·N превышает количество вершин в дереве. Дело в том, что при хранении дерева в массиве дети вершины с номером i лежат в ячейках с номерами 2·i и 2·i + 1 (если массив нумеруется с единицы), и при этом некоторые ячейки могут быть не задействованы.
Для примера рассмотрим случай N = 3. Дерево отрезков будет выглядеть следующим образом:
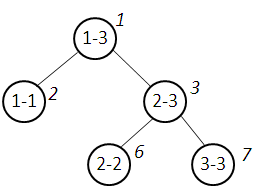
Внутри вершин написаны отрезки, которые данная вершина представляет. Рядом с каждой вершиной подписан её номер – он же индекс для хранения вершины в массиве. Номер корня равен 1, номера остальных вершин вычисляются по вышеприведённым формулам. Как видим, при хранении дерева в массиве ячейки 4 и 5 не используются, а последней задействованной ячейкой будет ячейка с номером 7.
Вам дан размер входного массива N. Определите номер последней задействованной ячейки массива, в котором будет храниться дерево (он же – наибольший номер вершины).
Одно натуральное число N (1 ≤ N ≤ 108).
Выведите одно натуральное число – номер последней задействованной ячейки массива для хранения дерева (оно же – максимальный номер вершины)
3
7
9
31
Можно заметить, что ответ зависит от того, как именно разбиваются отрезки нечётной длины при построении дерева. В данной задаче предполагается, что при разбиении отрезка нечётной длины левый подотрезок будет на единицу короче, чем правый (как и изображено на рисунке).
| © Copyright ВоГУ, АВТ, Носов Д.А., Смоленцев К.Н. |