|
English Russian |
Практикум по программированию |
| Вы не вошли в систему! Вход или регистрация. |
Треугольники
| Time limit: | 1 sec. |
| Memory limit: | 262144 KByte |
Одним ясным осенним днём Вася решил порисовать свои любимые правильные N-угольники. Нарисовав один из них, он выбрал три какие-то вершины и соединил их отрезками, получив тем самым треугольник. Затем Вася выбрал другую тройку вершин и получил другой треугольник, и так далее.
При этом Вася обратил внимание, что некоторые из полученных треугольников оказались равны. Например, треугольник 1-4-5 равен треугольнику 1-3-2, но не равен треугольнику 1-3-4.
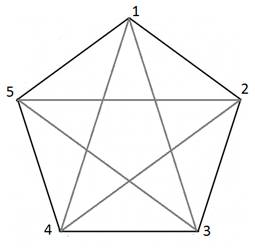
Вася заинтересовался, какое можно построить наибольшее количество треугольников, среди которых никакие два не равны друг другу. Например, для N=5 существует лишь два различных треугольника, а для N=6 их будет уже три.
Формат ответа.
Запишите в результирующий текстовый файл ровно пять чисел − ответы для N, равного:
· 7
· 10
· 2017
· 123456
· 987654321
Числа отделяйте друг от друга пробелом или переводом строки. Если вы не знаете все правильные ответы, то вместо недостающих напишите число 0.
Пример файла с ответами.
|
1 2 345 0 0 |
Примечание: в этом примере все ответы неверные
Система оценивания.
Каждый верный ответ оценивается в 20 баллов.
| © Copyright ВоГУ, АВТ, Носов Д.А., Смоленцев К.Н. |