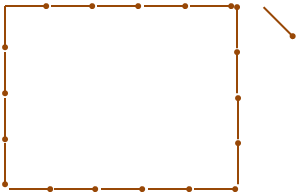
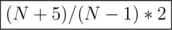Имеется N спичек. Требуется сложить из них прямоугольник, имеющий наибольшую площадь. Можно использовать не все спички.
Например, если N = 19, то максимальная площадь будет равна 20 у прямоугольника со сторонами 4 × 5. При этом одна спичка останется неиспользованной.
В данной задаче вам нужно придумать формулу, которая верно вычисляет максимально возможную площадь прямоугольника при любом
N ≥ 4.
Выходные данные
Вашим решением задачи должна быть одна строка с формулой.
В формуле вы можете использовать только следующие элементы:
- переменная N (заглавная латинская буква),
- любые целые числа от -1000 до 1000,
- круглые скобки,
- знаки бинарных операций '+', '-', '*', '/'. Здесь знак '/' означает деление нацело – например, 8 / 3 = 2, -8 / 3 = -2.
Приоритет операций умножения и деления нацело выше, чем у сложения и вычитания.
Дополнительные ограничения: длина вашей формулы не должна превышать 255 символов, промежуточные результаты вычисления не должны оказываться по модулю больше 109.
Пример, как может выглядеть запись формулы в ответе (этот ответ неправильный): 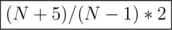
Система оценки
Правильность вашей формулы будет проверяться путём подстановки в неё различных значений N (4 ≤ N ≤ 1000). За каждый верный ответ начисляется определённое количество баллов. Максимальное количество баллов за задачу равно 100.