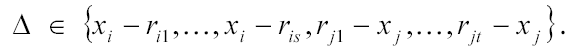Дистанционный практикум по программированию

Имеются три пробирки, вместимостью 100 миллилитров каждая. Первые две пробирки имеют риски, одинаковые на обеих пробирках. Возле каждой риски надписано целое число миллилитров, которое вмещается в часть пробирки от дна до этой риски (см. рисунок).

Изначально первая пробирка содержит 100 миллилитров пива, а остальные две пусты. Требуется написать программу, которая выясняет, можно ли отделить в третьей пробирке один миллилитр пива, и если да, то находит минимально необходимое для этого число переливаний. Пиво можно переливать из одной пробирки в другую до тех пор, пока либо первая из них не станет пустой, либо одна из пробирок не окажется заполненной до какой-либо риски.

Исходные данные

В первой строке входного файла содержится число рисок N (1 ≤ N ≤ 20), имеющихся на каждой из первых двух пробирок. Затем в порядке возрастания следуют N целых чисел V₁ , ..., V_N (1 ≤ V_i ≤ 100), приписанных рискам. Последняя риска считается сделанной на верхнем крае пробирок (V_N = 100).

Результат

В первой строке выходного файла должна содержаться строка YES, если в третьей пробирке возможно отделить один миллилитр пива, и NO - в противном случае. В случае ответа YES во вторую строку необходимо вывести искомое количество переливаний.

Пример

Решение

Рассмотрим более общий случай – для каждой пробирки имеется свой набор рисок, в который мы по соглашению дополнительно включаем риску со значением 0. Таким образом, для исходной задачи мы считаем, что третья пробирка имеет единственную «нулевую» риску.

Построим граф, изображающий возможные состояния набора из трех пробирок и возможные переходы между ними. Состояние задается тройкой неотрицательных целых чисел (x₁,x₂,x₃), где x_i – количество пива в пробирке i и x₁ + x₂ + x₃ = 100. Опишем теперь перечислитель вершин (x'₁,x'₂,x'₃) графа, в которые можно перейти из вершины (x₁,x₂,x₃) за одно переливание.

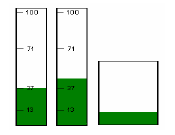
Рассмотрим, для определенности, случай переливания из пробирки i в пробирку j (1 ≤ i, j ≤ 3). Пусть в результате было перелито Δ миллилитров пива, т.е. 

x'_i = x_i - Δ,   x'_j = x_j - Δ,   x'_k = x_k,

где k = 6 - i - j. Наша задача сейчас – определить список возможных значений для Δ. Для этого обозначим через r_i1, ..., r_is те значения рисок пробирки i, которые меньше x_i, а через r_j1, ..., r_jt – те значения рисок пробирки j, которые меньше x_j. Ясно, что тогда 

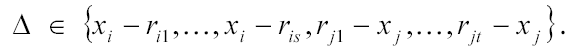
Далее осталось найти кратчайший путь в построенном графе, взяв в качестве начальной вершину (x₁,x₂,x₃ ), а в качестве конечных – вершины (x₁,x₂,x₃ ) с x₃ = 1.