Оргкомитет олимпиады по информатике решил наградить призёров
не только дипломами, но и медалями. При этом, чтобы подчеркнуть нестандартность
задач олимпиады, члены оргкомитета решили сделать и медали нестандартной формы.
В центре медали находится круг радиуса R.
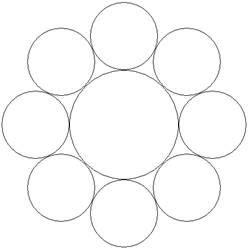
К нему примыкают N одинаковых
кругов так, что каждый из них касается не только центрального круга, но и двух
соседних. Пример для N = 8 показан
на рисунке.
Чтобы определить расход материала на изготовление такой
медали, нужно определить площадь её лицевой стороны. Напишите программу,
которая определяет суммарную площадь всех кругов.
Входные данные
Два разделённых пробелом целых числа R и N
(1 ≤ R ≤ 1000, 6 ≤ N ≤ 1000).
Выходные данные
Суммарная площадь всех кругов, округленная до
ближайшего целого числа.
Примечание: гарантируется, что во всех тестах задачи точное
значение площади отличается от ближайшего к нему целого числа не более чем на
0.49
|
Пример ввода
10
8
Пример вывода
1280
|

