Дистанционный практикум по программированию

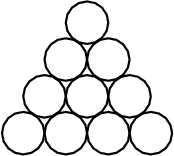
Рассмотрим фигуру из одинаковых кружочков, имеющую следующий вид.

Фигура состоит из n горизонтальных уровней, i-й из которых, в свою очередь, содержит i кружочков. Соседние кружочки на каждом уровне касаются; кроме того, для любого уровня i < n j-й кружочек i-го уровня касается j-го и (j + 1)-го кружочков (i + 1)-го уровня. Пример такой фигуры для n = 4 показан на рисунке. Уровни нумеруются с единицы сверху вниз; кружочки на одном уровне нумеруются с единицы слева направо.

Треугольником будем называть три попарно касающихся кружочка. Замощением фигуры треугольниками назовём разбиение множества всех кружочков фигуры на треугольники.

Будем записывать замощения следующим образом. Если у треугольника на более высоком уровне находится один кружочек, а на более низком — два, то кружочки, содержащиеся в этом треугольнике, обозначаются заглавной латинской буквой 'A'. Если же у треугольника на более высоком уровне два кружочка, а на более низком — один, то кружочки этого треугольника обозначаются заглавной латинской буквой 'B'. Сравнивать записи замощений будем как упорядоченные последовательности строк.

Рассмотрим все возможные замощения кружочками фигуры из n уровней; упорядочим их лексикографически. Выведите запись k-го в этом порядке замощения.

2 0

 A
A A