
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1276. POBEDA-2014
|
| Статистика | Послать на проверку | Задачу добавил Игорь Андрианов |
|
Как известно, современные видеокарты умеют формировать изображения с использованием только треугольников. Видеокарта POBEDA-2014 не отстает от современных тенденций. Известно, что она умеет отображать только прямоугольные равнобедренные треугольники четырех типов ориентации, представленные на рисунках ниже. Изменять ориентацию этих треугольников видеокарта не может. 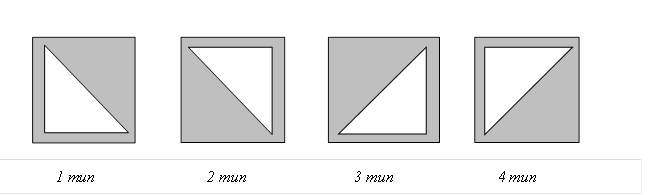
Длина катета каждого из представленных выше треугольников равна одному сантиметру. За один такт видеокарта не может отобразить более чем ai треугольников i-того типа. Необходимо определить максимально возможную длину стороны квадрата, который может быть изображен видеокартой на экране монитора за один такт. При этом квадрат должен быть расположен так, чтобы его стороны были параллельны краям монитора. Требуется написать программу, которая решает поставленную задачу. Формат входного файла Первая строка входного файла содержит разделенные пробелами четыре целых числа: a1, a2, a3, a4 (0 ≤ a1, a2, a3, a4 ≤ 1018). Входные данные могут превышать максимальные значения для 32 битного типа данных. Формат выходного файла Выходной файл должен содержать одно число – максимально возможную длину стороны квадрата. Примеры входных и выходных файлов
Пояснения к примерам Далее приведен рисунок для первого примера. 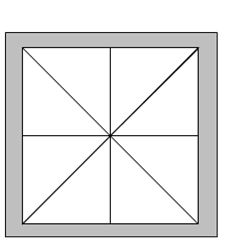
Система оценивания Частичные правильные решения для тестов, в которых a1, a2 ,a3 ,a4 ≤ 100 000, будут оцениваться из 50 баллов.
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Задачи с соревнований и сборов / | Школьные олимпиады и курсы Вологодской области / | ВсОШ, региональные этапы / | Региональный этап 2013-14 / |
| 1276. | 1277. 2 - Список школ | 1278. 3 - Межрегиональная олимпиада | 1279. 4 - Дом Мэра |
| время генерации 0.094 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |