
|
Дистанционный практикум по программированию
|
||||||||||
|
|
|||||||||||
| Здравствуйте, Гость! Войдите с паролем или зарегистрируйтесь. |
1260. Klingon Battle Bagel
|
| Статистика | Послать на проверку | Задачу добавил debug |
|
Two opponents play a game on a checkered field of size N×M. The first player places several shapes of “Klingon battle bagel” spaceship in the field. The shape of the ship is a solid 3 × 3 square having a hole in the center (see Fig.). 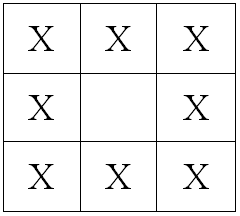 Ships can touch the edges of the field and each other but cannot intersect. The second player tries to find all the ships, firing at the cells of the field. The second player has made K shots at different cells hitting the ships, and F shots at other cells that missed. Write program to calculate the minimum and the maximum number of ships that can be located in the field.
InputThe number of rows N and the number of columns M of the playing field are given in the first line of the input file, separated with a space character. The second line contains the number of hits H and the number of misses F.
OutputSpace-delimited values of the minimum and the maximum number of ships possibly located on the field. Output “BAZINGA!” (without quotation marks) if no solution exists for the input data.
Limitations1 ≤ N, M ≤ 100 000. 0 ≤ H, F ≤ N×M.
Example
|
| Статистика | Послать на проверку | Обсуждение задачи | Автор/источник: |
| Задачи с соревнований и сборов / | Чемпионат мира по программированию (ICPC) / | Рыбинск-2013 / |
| 1259. H - Redirect | 1260. | 1261. J - Meteorite | 1262. K - Triangles |
| время генерации 0.141 сек. | |
| © Copyright ВоГУ, АВТ, Носов Д.А., Андрианов И.А. |