|
Одним пасмурным осенним днём Вася решил порисовать
свои любимые правильные N-угольники. Нарисовав один из них, он решил провести в
нём все возможные диагонали — отрезки, соединяющие не соседние вершины. Рисунок
ему очень понравился, особенно расположение точек, в которых пересекались
диагонали. В этом было что-то загадочное. Вася решил, что чем больше этих точек
— тем красивее получается рисунок.
Ваша задача — подсчитать количество точек пересечения
диагоналей, лежащих строго внутри правильного N-угольника с
нечётным количеством сторон. Известно, что при нечётном количестве сторон нет точек,
в которых бы пересекались больше двух диагоналей.
В первой строке входных данных дано число N (5 ≤ N ≤ 55 055) —
количество сторон в правильном многоугольнике, N
нечётное.
Выведите количество точек пересечения
диагоналей, лежащих строго внутри правильного N-угольника.
|
Пример ввода 1
5
Пример вывода 1
5
|
Пример ввода 2
7
Пример вывода 2
35
|
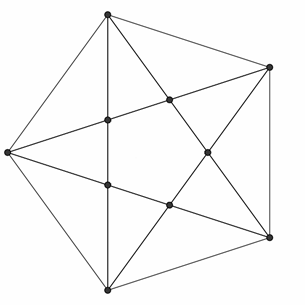
Пояснение.
В первом примере описан правильный пятиугольник, в котором проведены 5
диагоналей. Количество точек пересечения, лежащих строго внутри него, равно 5.
| 
